文章图片
文章图片
文章图片
文章图片
文章图片
机器之心报道
机器之心编辑部
LoRA 在绝大多数后训练场景下 , 能以远低于全量微调的成本 , 获得几乎同等的效果 。 Thinking Machines 将这一现象形容为 LoRA 的低遗憾区间(low-regret region)——即便不用全量微调 , 选择 LoRA 也不会让人后悔 。
最近 , Thinking Machines 真实高产啊 。
今天 , 他们又更新了博客 , 力推 LoRA , 且与全量微调( Full Fine-tuning, 以下简称 FullFT )进行了对比 。
博客链接: https://thinkingmachines.ai/blog/lora/训练大模型 , 到底该选全量微调还是 LoRA?
FullFT 意味着改动模型的所有参数 , 效果稳定但成本高昂 , 显存开销巨大;而LoRA 只改动一小部分参数 , 轻量、便宜 。 但一个关键问题是:便宜的 LoRA , 效果会不会差很多?
Thinking Machines 最新研究发现 , 在小数据量任务上 , LoRA 与 FullFT 几乎没有差距 , 完全可以对齐;在大数据量任务上 , LoRA 的容量不足 , 承载不了过多新知识 , 表现略显吃力;而在强化学习任务里 , 哪怕 LoRA rank=1 这么小的设定 , 也能跑出与全量微调接近的效果 。
更进一步 , LoRA 的使用位置也有讲究 。 只加在注意力层并不理想 , 覆盖所有层(尤其 MLP/MoE)效果更佳 。
研究还揭示了一些细节差异 。 例如 , LoRA 在大 batch size 下 , 比 FullFT 更容易掉性能;LoRA 的学习率和超参数规律与 FullFT 不同 , 需要单独调优 。
以下是这篇博客的主要内容 。
为什么 LoRA 重要?
低秩适配( LoRA )是目前最热门的参数高效微调(PEFT)方法 。 它的核心思想是:不直接改动整个模型的权重 , 而是通过学习一个低维适配器(两个小矩阵 A 和 B)来表示更新 。
LoRA 的优势包括:多租户部署(同一模型可同时加载多个适配器)、低显存需求、快速加载和迁移 。 这些特性让它自 2021 年诞生以来迅速流行 。
不过 , 现有研究对它能否完全匹敌 FullFT 并没有一致答案 。
学界普遍认为 , 在类似预训练的大规模数据场景下 , LoRA 性能会逊于 FullFT, 因为数据规模往往超出 LoRA 参数容量 。 但在后训练任务中 , 数据规模通常处于 LoRA 容量可覆盖的范围 , 这意味着核心信息能够被保留 。
尽管如此 , 这并不必然保证 LoRA 在样本利用效率和计算效率上能完全与 FullFT 持平 。 我们关注的核心问题是:
在什么条件下 , LoRA 能实现与 FullFT 相当的效果?
实验结果显示 , 只要关键细节得到妥善处理 , LoRA 不仅能匹配 FullFT 的样本效率 , 还能最终达到相似的性能水平 。
LoRA 的关键要素
研究的方法有别于以往研究:
不再局限于单一数据集或任务 , 而是系统考察训练集规模与 LoRA 参数数量之间的普适关系;在有监督学习中 , 研究采用对数损失(log loss)作为统一评估指标 , 而非依赖采样式评测 , 以获得更清晰且可跨任务比较的结论 。
实验结果表明 , 在小到中等规模的指令微调和推理任务中 , LoRA 的表现可与FullFT 相媲美 。 然而 , 当数据规模超出 LoRA 参数容量时 , 其表现将落后于 FullFT , 这种差距主要体现在训练效率的下降 , 而非无法继续优化 。 性能下降的程度与模型容量和数据规模密切相关 。
此外 , LoRA 对大批量训练的容忍度低于 FullFT。 当批量规模超过一定阈值时 , 损失值会明显上升 , 这种现象无法通过提升 LoRA 的秩(rank)来缓解 , 因为它源自矩阵乘积参数化的固有训练动力学 , 而非原始权重矩阵的直接优化 。
即便在小数据场景 , 将 LoRA 应用于所有权重矩阵 , 尤其是 MLP 与 MoE 层 , 均能获得更优表现 。 相比之下 , 仅对注意力层进行 LoRA 调整 , 即使保持相同可训练参数量 , 也无法达到同样的效果 。
在强化学习任务中 , 即使 LoRA 的秩(rank)极低 , 其性能仍可接近 FullFT。 这与我们基于信息论的推断一致:强化学习对模型容量的需求相对较低 。
研究还分析了 LoRA 超参数对学习率的影响 , 包括初始化尺度与乘数的不变性 , 并揭示了为何 1/r1/r1/r 因子使 LoRA 的最优学习率与秩变化几乎无关 。 同时实验显示 , LoRA 的最优学习率与 FullFT 存在一定关联 。
综合来看 , 研究提出了低遗憾区域(low-regret region)的概念——
在该区域内 , 大多数后训练场景下 , LoRA 能以显著低于 FullFT 的成本 , 实现相似的性能 。 这意味着 , 高效微调在实际应用中完全可行 , LoRA 因而成为后训练的重要工具 。
实验方法与主要发现
研究团队用 LLaMA 3 和 Qwen3 模型 , 做了有监督微调(Tulu3 和 OpenThoughts3 数据集)以及强化学习任务(数学推理) 。 关键做法包括:
调整 LoRA 的秩(rank) , 从 1 到 512 , 覆盖从低容量到高容量的场景 。 对每个设置做学习率扫描 , 确保找到最优训练条件 。 测试 LoRA 在不同层的效果 , 包括 attention 层、MLP 层、混合专家(MoE)层 。结果发现:
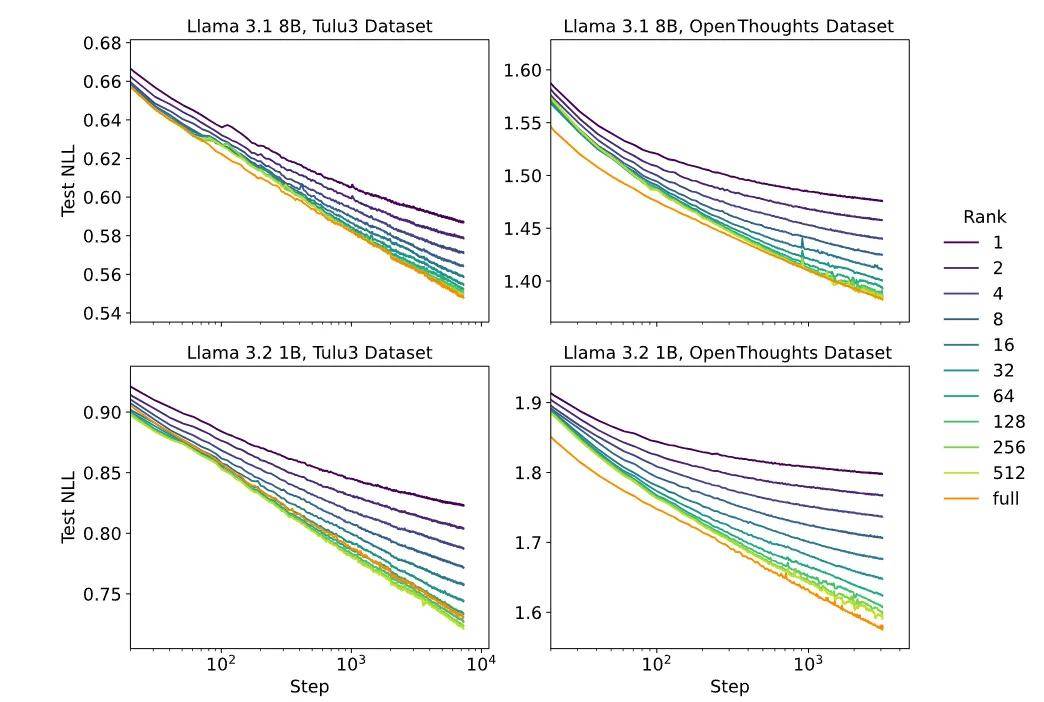
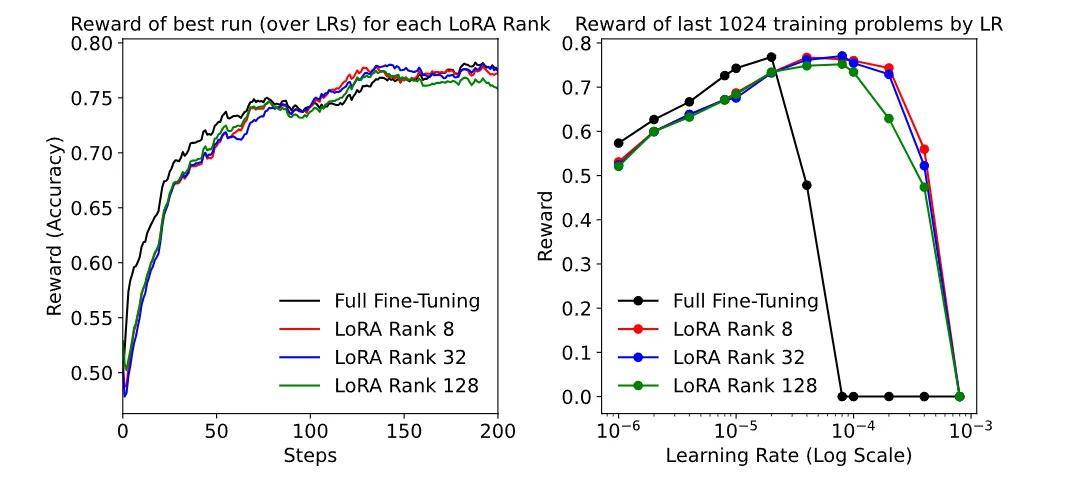
在小到中等数据规模下 , 高秩 LoRA 的性能几乎与 FullFT 无差别 。
在 Tulu3 和 OpenThoughts3 数据集上 , 全量微调(FullFT)以及高秩 LoRA 的学习曲线非常相似 , 损失随训练步骤的对数几乎线性下降 。 而低秩 LoRA 则会在适配器容量耗尽时偏离最小损失曲线 。 在底部的图表(1B 模型)中 , 高秩 LoRA 在某个数据集上表现优于 FullFT , 但在另一个数据集上则略逊一筹 。 这可能与不同数据集的训练动态或泛化行为差异有关 , 从而导致 LoRA 在不同任务上的表现存在一定随机性 。
结果显示 , 对于 Tulu3 数据集 , 不同秩的 LoRA 在最佳学习率下的最终损失相差不大 , 高秩 LoRA 与 FullFT 的最小损失几乎一致 。 然而 , LoRA 的最佳学习率约是 FullFT 的 10 倍 , 这意味着在相同条件下 LoRA 可以接受更高的学习率 。
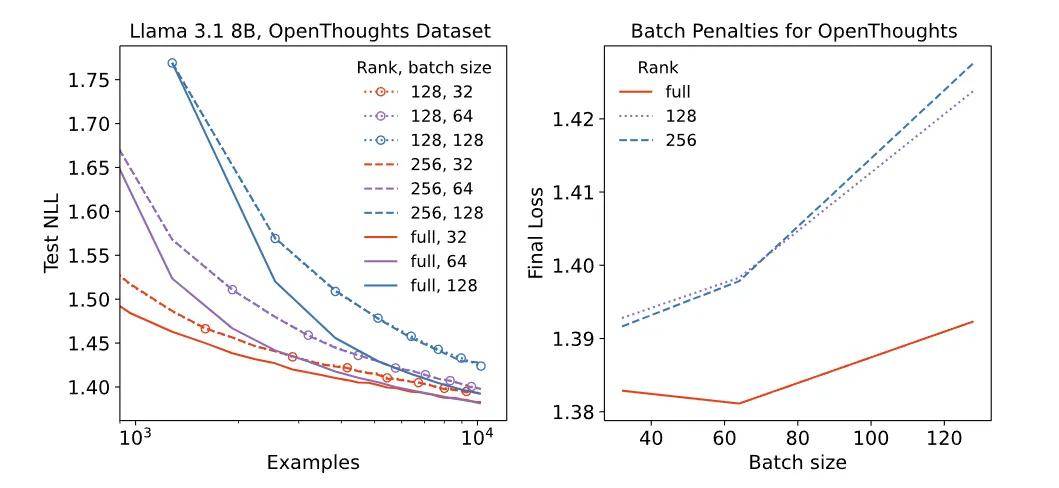
对于超过 LoRA 容量的数据集 , LoRA 的表现不如 FullFT 。损失并不会达到一个无法降低的明显下限 , 而是会导致更差的训练效率 , 这种效率取决于模型容量与数据集大小之间的关系 。 大批量训练下 , LoRA 性能下降比 FullFT 更明显 , 这与秩无关 , 可能是参数化方法的固有特性 。
批量大小对 LoRA 与 FullFT 性能的影响如图所示 。 左侧的学习曲线展示了在不同批量大小下的表现:在较大批量情况下 , LoRA(虚线)的学习曲线始终低于 FullFT(实线) , 表现出持续的差距 。 右侧的图表则展示了最终损失与批量大小的关系 , 表明随着批量大小的增加 , LoRA 所付出的损失代价更大 。
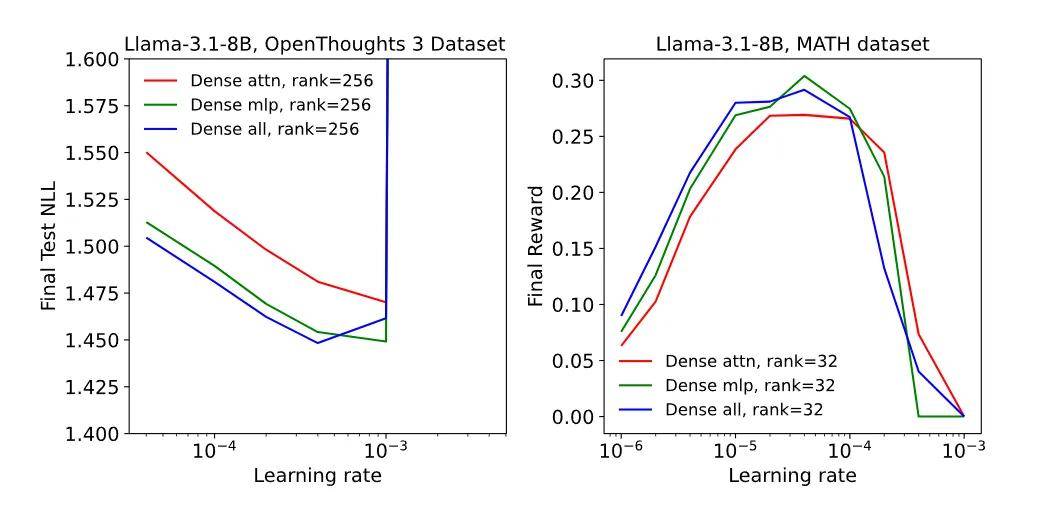
即使在数据量小的情境下 , LoRA 在应用于所有权重矩阵(特别是 MLP 和 MoE 层)时表现更好 。 仅应用于注意力层的 LoRA(attention-only LoRA)表现不佳 , 即使研究人员通过使用更高的秩来匹配可训练参数的数量(与 MLP-only 相比) 。
仅作用于注意力层的 LoRA(Attention-only LoRA)明显不如仅作用于 MLP 层的 LoRA(MLP-only LoRA) , 而且在已对 MLP 层应用 LoRA 的情况下 , 再对注意力层额外应用 LoRA 并不能进一步提升性能 。 这一现象在密集模型(如 Llama-3.1-8B)和稀疏 MoE 模型(如 Qwen3-30B-A3B-Base)中均成立 。
改变应用 LoRA 的层时 , 学习率与最终损失或奖励的关系 。
在强化学习任务中 , 即使秩极低(rank=1) , LoRA 也能达到 FullFT 水平 , 这与强化学习对容量需求较低的理论预期一致 。
在小学数学(GSM , 左图)或 MATH(右图)数据集上进行强化学习时 , 学习率与最终奖励(准确率)的关系 。
在 DeepMath 数据集上使用 Qwen3-8b-base 进行的实验 。 左图显示了不同 rank 和全量微调(FullFT)的学习曲线 。 在每种设置下 , 我们选取了能带来最佳最终性能的最优学习率 。 右图则展示了学习率与最终性能的关系 。 与之前的数学实验类似 , LoRA 在近似最优学习率范围上表现出更宽的峰值 。
来自使用 Qwen3-8b-Base 在 DeepMath 数据集上实验的附加图表 。 左图显示了在更具挑战性的 AIME 测试集上的基准得分 , 右图展示了随训练步骤变化的链式思维(CoT)长度 , 这可被视为模型学习推理能力的一个标志 。
LoRA 超参数规律
LoRA 有几个显著特点 , 简化了它的使用复杂度:
最优学习率通常是 FullFT 的 约 10 倍 。 学习率对秩的依赖非常弱 , 短期训练几乎不受秩变化影响 , 长期训练差异也很小 。 LoRA 参数化具有不变性 , 实际只需关注两个组合超参数即可 。 初期训练时 , LoRA 需要更高的学习率(约 15 倍 FullFT) , 长期训练则趋近于 10 倍 。这些规律为 LoRA 在实际部署中提供了便利:少调超参数就能取得接近全量微调的效果 。
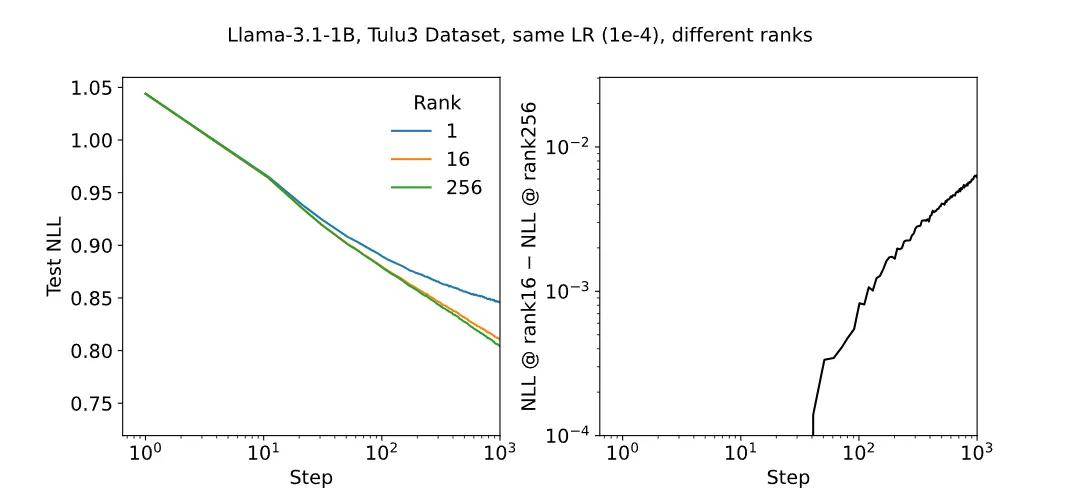
训练早期 , 不同 rank 在相同学习率下的学习曲线差异 。 左图显示了各 rank 的学习曲线 , 右图则展示了 rank?16 与 rank?256 之间的差异 , 这个差异随时间增长 。 有趣的是 , 在最初几步中差异为负(尽管非常微?。 ?, 因此那部分曲线在图中缺失 。
讨论
1、为什么 LoRA 必须作用于所有层?我们发现 , LoRA 要与 FullFT 接近 , 必须满足两个条件:作用于所有层 , 特别是 MLP/MoE 层 , 因为这些层承载了模型绝大部分参数 。 容量不受限制 , 可训练参数必须足够容纳数据中所需的信息量 。
仅在 attention 层使用 LoRA 会导致训练速度下降 , 这可以用经验神经切线核(eNTK)解释:参数最多的层对训练动态影响最大 , LoRA 覆盖所有参数层 , 才能保持 FullFT 的训练行为 。
2、我们用信息论方法估算了容量需求 , 这种分析为 LoRA 在不同任务中能否胜任提供了理论支持:
在监督学习中 , 模型大约可存储每个参数 2 bits 信息 。 数据集的描述长度可以通过第一轮训练的总 log-loss 估算;
在强化学习中 , 尤其是策略梯度方法 , 每个 episode 约提供 1 bit 信息 。 这说明强化学习对 LoRA 容量的要求相对较低 。
3、计算效率优势 。 LoRA 只更新低秩矩阵 , 而不是全权重矩阵 , 这让它在计算上更省力:前向+反向传播的 FLOPs 大约是 FullFT 的 2/3 。
换句话说 , LoRA 在相同训练步骤下 , 能用更少计算量达到相似效果 。
未来探索方向
【Thinking Machines又发高质量博客:力推LoRA,不输全量微调】研究团队认为 , LoRA 仍有几个值得深入探索的方向:精准预测 LoRA 性能及其与 FullFT 的差距条件、建立 LoRA 学习率与训练动态的理论框架、测评 LoRA 变体(如 PiSSA)的表现 , 以及研究 LoRA 在 MoE 层的不同应用方案及其与张量并行、专家并行的兼容性 。
推荐阅读
- 陈丹琦,入职Thinking Machines Lab了?
- 999元,小米又发布新机,这次主打学习!
- 美国把机器狗藏着当宝,中国又发布了机器狼,机器狗安排扫垃圾了
- 大快人心!中国又发生一件让美国恐惧的大事!
- 又发簪怎么盘丸子头教学













