GPT-5 Pro独立做数学研究，OpenAI总裁：这是生命迹象_芯片|ai|it芯片

文章图片

文章图片

文章图片

文章图片

克雷西发自凹非寺
量子位 | 公众号 QbitAI
AI已经能够自主思考并证明新的数学规律了？
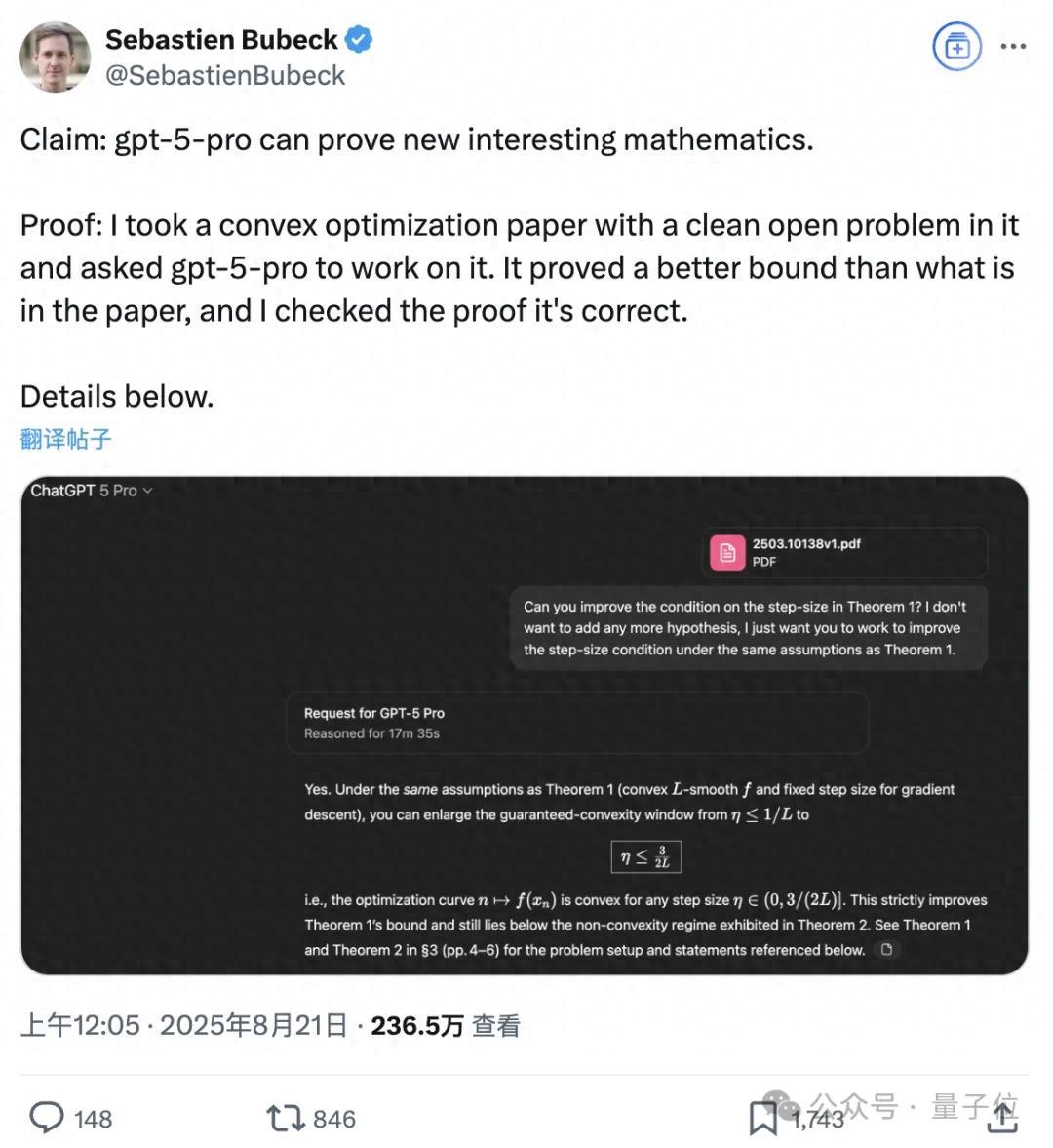
OpenAI研究人员表示，自己喂给GPT-5 Pro一篇论文，结果模型读完之后得到了新的结论。
在凸优化问题当中， GPT-5 Pro针对一个边界问题，给出了比原文更加精确的阈值和相应证明。
消息立即引发全网热议，不到半天推文就有230多万次阅读。

不过这位研究人员并没有将GPT-5 Pro的研究成果发表成论文，理由是被人类抢先了——
这篇论文后来又更新了一个版本，给出了新的边界，这个新的边界又把GPT-5 Pro反超了。
但是， GPT-5 Pro的证明思路与此并不相同，说明它已经具备了独立探索的能力，所以人类的反攻也不影响这是GPT-5 Pro的一个新突破。
OpenAI总裁Brockman甚至将这一成果称之为“生命迹象” 。

凸优化曲线是凸的吗？喂给GPT-5 Pro的这篇另论文，研究的是凸优化（convex optimization）问题，凸优化是数学最优化的一个子领域，研究定义于凸集中的凸函数最小化的问题。
具体来说，这篇论文题目为《凸优化曲线是凸的吗？》，研究了这样的一个问题：
当使用梯度下降算法优化光滑凸函数时，其产生的优化曲线（optimization curve）是否是凸的？
这里的“优化曲线”指的是函数值f(x_n)随迭代次数n变化的曲线。如果这条曲线是凸的，意味着优化速率（即相邻两次迭代的函数值下降量）是单调递减的。
【GPT-5 Pro独立做数学研究，OpenAI总裁：这是生命迹象】
关于这个问题，论文的结论是优化曲线凸不凸，关键取决于步长（step size）的选择，具体包括如下几个关键点：
凸性保证区间：当步长η ∈ (0 1/L
时（L为平滑度），优化曲线保证是凸的；非凸可能区间：当步长η ∈ (1.75/L 2/L)时，即使梯度下降仍单调收敛，优化曲线可能不是凸的；梯度范数性质：对于整个收敛区间η ∈ (0 2/L
，梯度范数序列||?f(x_n)||总是单调递减的；二阶可导凸函数的梯度流凸性：对于凸且二阶连续可导的函数，梯度流的优化曲线总是凸的；光滑凸函数的梯度流凸性：对于凸L-光滑函数（不要求二阶可导），梯度流的优化曲线总是凸的；梯度流的梯度范数单调性：对于连续时间的梯度流，优化曲线总是凸的；关于第一个结论，证明的核心是证明序列{f(x_n) - f[(x_(n+1)
非递增。
论文作者巧妙地引入辅助函数g_k(t) ，将离散的迭代过程转化为连续函数的积分，利用凸函数的性质证明辅助函数的单调性，通过比较相邻两个辅助函数的大小关系，最终证明优化曲线的凸性。

非凸可能区间部分则是构造一个分段函数（二次函数和线性函数的组合）作为反例实现证明。
作者选择特定的初始点x_0 = -1.8 ，通过直接计算前三步迭代的函数值下降量，验证在该步长范围内，后面的下降量反而比前面大，违反了凸性要求。

由于GPT-5 Pro的证明主要针对的是边界问题，后面四个结论的证明过程在这里就不详细介绍了，感兴趣的话可以阅读原论文。
GPT-5 Pro给出新边界在论文的第一版中，作者分别证明了步长不大于1/L和大于1.75/L时的情况，但在(1/L 1.75/L
范围内则未有定论。
GPT-5 Pro则是通过更精细的不等式技巧，用17分半的时间把1/L这个边界移动到了1.5/L 。
而人类检查证明过程的时间，是25分钟， GPT-5 Pro读论文并进行证明的时间还要长。

其核心思路与原论文相似，均是将优化曲线凸性问题转化为证明函数值下降量递减。
但GPT-5 Pro巧妙运用了凸L-光滑函数的两个基本不等式——Bregman散度不等式（提供更紧的下界）和标准的共强制性（cocoercivity）不等式。
通过这种巧妙的代数操作， GPT-5 Pro成功将凸性条件进一步细化。

再之后， GPT-5 Pro的发现还未来得及发表，论文原作者就对论文进行了更新，作者新增了一名，关键是证明了1.75/L就是一个精确界限，之前未探索的区间实现了闭合。
其思路是利用凸L-光滑函数的Bregman散度不等式，对三个点对(x_0x_1)、(x_1x_2)和(x_0x_2) 分别建立不等式，之后将三个不等式分别乘以不同权重后求和，并通过恒等式将复杂的梯度项组合化简。

虽然GPT-5 Pro给出的证明最后被人类扳回一城，但是，其思路和过程与新版论文不同。
也就是说， GPT-5 Pro并不是发现了新论文才实现边界的精确化，而是确实具备了自主发现并证明数学规律的能力。
参考链接：[1
https://x.com/SebastienBubeck/status/1958198661139009862[2
https://arxiv.org/abs/2503.10138v1[3
https://arxiv.org/abs/2503.10138v2
— 完 —
量子位 QbitAI
关注我们，第一时间获知前沿科技动态

GPT-5 Pro独立做数学研究，OpenAI总裁：这是生命迹象

推荐阅读

土壤改良有什么技术

武汉积分落户什么时候出结果

gl8经典变速箱油多久换一次？

芝士的热量

做假水的简单方法不用胶水做假水的简单方法

怎么改变小孩拖拉问题怎么改变小孩拖拉问题的毛病

梦见香蕉梦见香蕉是什么意思

甘蓝炒肉片的做法甘蓝炒肉片怎么做

如何自制盐焗鸡

离家一个月冰箱要断电吗

t2太耗电

怎么选择板材

小学三年级作文一件有趣的事作文500字

天翼手机卡，中国电信天翼卡

改善皮肤粗糙的方法改善皮肤粗糙

螺丝尾巴剪了放一晚上会死吗