斯坦福：优化器「诸神之战」？AdamW 凭「稳定」胜出_客服|人工智能

文章图片

文章图片

文章图片

文章图片

机器之心报道
机器之心编辑部
自 2014 年提出以来， Adam 及其改进版 AdamW 长期占据开放权重语言模型预训练的主导地位，帮助模型在海量数据下保持稳定并实现较快收敛。
随着模型规模迅速扩大，预训练已成为计算密集型任务的典型代表，在大模型研发中往往是最主要的计算开销。在这种背景下，优化器的设计直接关系到收敛速度与计算成本。
研究者们探索了多种改进方向，其中最快的优化器往往采用矩阵型预条件子（如 Muon、Soap、Kron），相较于经过严格调优的 AdamW ，可以带来约 30–40% 的迭代级别加速。
斯坦福大学 Percy Liang 团队的研究指出，尽管存在许多声称能提供显著加速（1.4 至 2 倍）的替代方案， AdamW 依然是预训练的稳健首选，但矩阵型方法在特定数据–模型比例下展现出明显优势。

论文标题：Fantastic Pretraining Optimizers and Where to Find Them 论文地址：https://www.arxiv.org/pdf/2509.02046v1 Github：https://github.com/marin-community/marin/issues/1290 博客：https://wandb.ai/marin-community/marin/reports/Fantastic-Optimizers-and-Where-to-Find-Them--VmlldzoxMjgzMzQ2NQ研究者认为，这种现象可能源于两个关键的方法论缺陷：
问题 1：不公平的超参数调优。基线模型通常调优不足：在常用的 AdamW 基线中，仅仅是调优学习率这一个参数，就能在 1.3 亿参数规模的模型上实现 2 倍的加速。
固定共享的超参数并不能保证比较的公平性：例如，与标准的权重衰减值 0.1 相比， Lion 优化器更偏好较高的权重衰减值（如 0.6）。

左：常用的 AdamW 基线存在调优不足的问题。在 Brown 等人 [2020
提出、并被后续多项研究采用的 GPT-3 训练方案中，仅仅针对一个 1 亿参数的模型调整学习率这一个超参数，便可实现高达 2 倍的加速，这凸显了进行恰当超参数优化的重要性。右：在不同优化器之间固定超参数并不能保证比较的公平性。在以往的研究中，像学习率和权重衰减这类共享超参数通常被设为常量。然而，即使是概念上相似的优化器，其对应的最优超参数也可能大相径庭。
问题 2：测试规模不足大多数测试仅使用小型模型（参数远小于 10 亿）或遵循 Chinchilla 论文提出的 1 倍数据配比。那么，在更大规模的模型或更高的数据配比下，结果会如何呢？
此外，训练早期的检查点也可能产生误导，在学习率衰减阶段，不同方法的损失曲线可能会发生交叉，从而导致最终排名反转。因此，必须在（不同的）设定下进行训练结束时的最终评估。

左：加速效果随模型规模的增大而衰减。尽管一些优化器在参数量小于 10 亿的模型上相比 AdamW 能展现出较高的加速比（1.3-1.4 倍），但当模型规模增至 12 亿参数时，其加速比会衰减至仅 1.1 倍。右：基于矩阵的优化器性能稳定优于基于标量的优化器。该图展示了三种基于标量的优化器（AdamW Nesterov AdamW Mars）和三种基于矩阵的优化器（Kron Soap Muon）在不同 Chinchilla 数据配比下训练时的损失曲线。基于矩阵的优化器相比基于标量的优化器实现了一致的加速效果。此外，在过训练（overtrained）的情况下，这三种基于矩阵的优化器最终会收敛到相似的损失值。
为了验证这一假设，研究人员进行了系统性的比较研究，涵盖了十一种不同的深度学习优化器。他们在多种模型规模（从 1 亿到 12 亿参数）和数据–模型比例（参照 Chinchilla 最优比例的 1 倍至 8 倍）下，为每一种优化器都进行了严谨、独立的超参数调优。

本研究所使用的优化器。
研究发现：
独立调优至关重要：一个优化器的最优超参数配置往往无法直接迁移到另一种优化器上。如果缺乏独立调优，不仅比较结果缺乏公平性，而且新优化器相较于精心调优过的 AdamW ，实际加速效果远低于其声称的数值。短期评估具有误导性：仅在短时间训练窗口内评估优化器性能是不可靠的。随着训练的进行和学习率衰减，不同优化器的性能排名可能会发生逆转，其损失曲线甚至会多次交叉。矩阵方法性能领先：所有速度最快的优化器都采用了基于矩阵的预条件子，而非传统的逐元素标量缩放。 Muon、Soap 和 Kron 等方法，相比严格调优后的 AdamW ，能够实现 30–40% 的单步训练速度提升。有趣的是，最优选择也与具体场景相关：在标准 Chinchilla 数据比例下， Muon 表现最佳；而当数据量相对于模型规模的比例提升至 8 倍以上时， Soap 则成为更优的选择。

方法
研究设计了一套严谨的方法论来评估这些优化器，该方法分为三个主要阶段。首先是通用设置阶段，明确了实验环境。研究使用了四种不同规模的 Transformer 模型，参数量从 130M 到 1.2B ，序列长度均为 4096 ，并详细列举了各模型层数、隐藏维度等具体配置。

所研究的各个模型规模的详细架构超参数。
数据方面，研究混合使用了 DCLM-baseline、StarCoder V2 和 ProofPile 2 数据集，并使用 LLaMA-3 分词器进行分词，确保了训练数据的丰富性。评估的优化器涵盖了 AdamW、NAdamW、Mars、Cautious、Lion、Adam-mini、Muon、Scion、Kron (PSGD) 、Soap 和 Sophia ，代表了当前深度学习优化领域的主流和前沿方法。
阶段 I: 全面参数扫描
研究旨在解决基线优化器超参数调整不当导致其性能被低估的问题。研究采用了坐标下降法，对所有优化器的超参数（包括学习率、权重衰减、预热步数、β?、β?、ε、最大梯度范数和批次大?。 ┰谠ど柰裆辖辛讼昃∷阉?。
这一阶段的实验设置涵盖了 130M、300M 和 500M 模型在 1 倍 Chinchilla 数据量下的训练，以及 130M 模型在 2 倍、4 倍、8 倍 Chinchilla 数据量下的训练。
研究发现，对每个优化器进行严格的超参数调整至关重要，因为不同优化器之间的最优超参数配置差异显著，盲目迁移超参数会导致不公平的比较。
此外，研究也观察到，与经过精心调整的基线 AdamW 相比，实际的加速效果普遍低于此前一些研究所声称的水平。
阶段 II: 敏感超参数识别
研究根据第一阶段的结果，识别出那些最优值会随模型规模变化的敏感超参数，例如学习率和预热长度。随后，这些敏感超参数在 300M 和 500M 模型以及 2 倍、4 倍、8 倍 Chinchilla 数据量下进行了进一步的网格搜索。

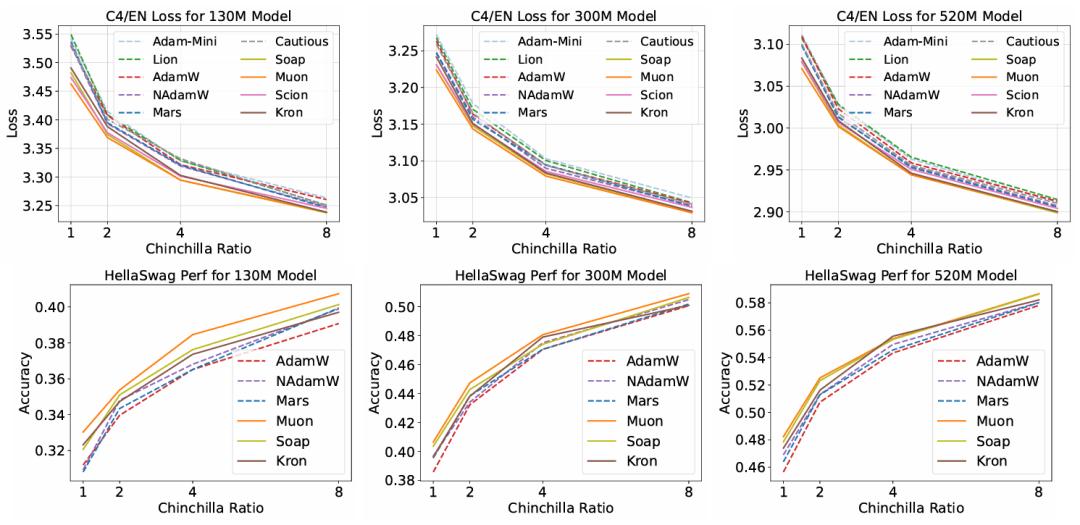
第一阶段与第二阶段的主要结果。上图：我们绘制了第一阶段和第二阶段实验中，模型在 C4/EN 数据集上的验证集损失。图中的每一个点都对应于每种优化器在相应的 Chinchilla 数据配比下所能达到的最优损失值。下图：我们针对部分优化器，绘制了它们在 HellaSwag 基准上的性能。这些优化器包括：AdamW 基线、性能排名前 2 的基于标量的优化器，以及性能排名前 3 的基于矩阵的优化器。性能数据来自于它们各自最优的运行批次。
通过结合前两个阶段的结果，研究获得了 12 种不同设置下的近乎最优超参数集及其对应的损失。为了量化不同优化器相对于 AdamW 的加速效果，研究拟合了 AdamW 损失随数据预算变化的缩放定律，并以此计算出达到相同损失所需的 AdamW 数据量与优化器实际所需数据量之比，作为加速比。
研究发现，基于矩阵的优化器虽然表现普遍优于基于标量的优化器，但其加速比在实际测试中均未超过 1.4 倍。许多替代优化器在小规模模型或有限数据比例下看似具有优势，但随着模型规模扩大，这些加速优势逐渐消失甚至反转， AdamW 依然是最稳健的预训练首选。
阶段 III: 案例研究
该阶段旨在对更大规模的实验进行深入探索。研究首先检验了超参数的拟合程度，通过拟合形式为的平滑定律，预测了在模型规模 N 和数据规模 D 下的最优设置。

为了验证这些缩放定律，研究对 1.2B 模型在 1 倍 Chinchilla 数据量下进行了全面扫描，结果显示预测的配置与实际最优配置之间的性能差异极小，证明了预测的有效性。
随后，研究进行了两项案例研究：一是训练 1.2B 模型在 1 至 8 倍 Chinchilla 数据量下，以检验优化器加速效果随模型规模扩展的变化；二是在 16 倍 Chinchilla 数据量下训练 130M 和 300M 模型，以观察在极端数据量与模型比例下的优化器表现。

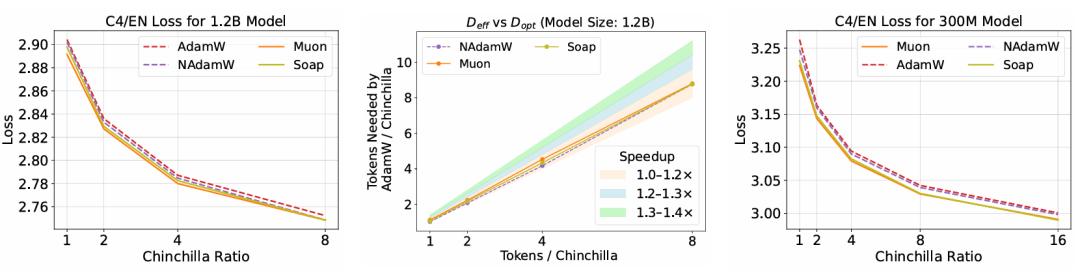
案例分析。左图：在 12 亿参数模型上， AdamW、NAdamW、Muon 和 Soap 四种优化器的验证集损失缩放情况。结果显示， Muon 和 Soap 相比 AdamW 仍有显著的加速效果，但相比 NAdamW 已无明显加速优势。中图：采用与图 3 相同的方法估算加速比。我们观察到， Muon 和 Soap 的加速比随模型规模增大而衰减，最终降至仅 1.1 倍。右图：在 3 亿参数模型和 16 倍 Chinchilla 数据配比的设定下，实验结果表明，当数据与模型的比例进一步增大时， Soap 的性能优于 Muon 。
这一阶段的结果进一步揭示了 Muon 优化器的潜在局限性：尽管 Muon 对高达 1.2B 参数的模型仍有加速效果，但加速比会下降到 1.2 倍以下。在高数据与模型比例（如 16 倍 Chinchilla）下， NAdamW 和 Soap 在 130M 模型上超越了 Muon ，且 Soap 在 300M 模型上也超过了 Muon 。研究推测，在数据与模型比例很高时， Soap 和 Kron 所维持的二阶动量变得更为有效。
【斯坦福：优化器「诸神之战」？AdamW 凭「稳定」胜出】更多细节请阅读原论文。

斯坦福：优化器「诸神之战」？AdamW 凭「稳定」胜出

推荐阅读

6寸是多少厘米 6寸照片尺寸是多大

对资产的贪污和盗用会导致

房贷要不要提前还房贷本金提前还款划算吗？

厕所堵了要怎么弄快速解决

忘忧草代表什么意思忘忧草象征什么

婴儿吓着了怎么办被吓到解决方法

众志成城抗击疫情手抄报众志成城抗击疫情手抄报画法

有什么好看的电影吗好看的电影推荐

梦见看见小偷梦见看见小偷偷东西

西门子洗衣机iq300童锁解除

已婚男人在外动了情已婚男人动了情很可怕

巨蟹男知道你喜欢他后，巨蟹男真心喜欢你的表现

蒋卉，郑伟的父母是谁

母亲节收到的礼物母亲节收到女儿礼物感言

黄仁勋为什么老是穿皮夹克,飞行员为什么穿皮衣

为什么钩尖江湖更新特别慢，为啥更新那么慢