经典ReLU回归！重大缺陷「死亡ReLU问题」已被解决

文章图片

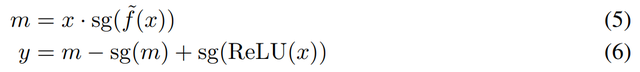
文章图片

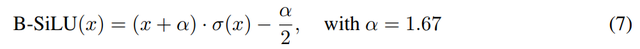
文章图片

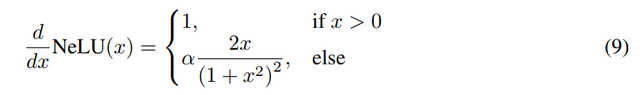
文章图片

文章图片

机器之心报道
机器之心编辑部

【经典ReLU回归！重大缺陷「死亡ReLU问题」已被解决】不用换模型、不用堆参数，靠 SUGAR 模型性能大增！

在深度学习领域中，对激活函数的探讨已成为一个独立的研究方向。例如 GELU、SELU 和 SiLU 等函数凭借其平滑梯度与卓越的收敛特性，已成为热门选择。

尽管这一趋势盛行，经典 ReLU 函数仍因其简洁性、固有稀疏性及其他优势拓扑特性而广受青睐。

然而 ReLU 单元易陷入所谓的「死亡 ReLU 问题」，一旦某个神经元在训练中输出恒为 0 ，其梯度也为 0 ，无法再恢复。这一现象最终制约了其整体效能，也是 ReLU 网络的重大缺陷。

正是死亡 ReLU 问题催生了大量改进的线性单元函数，包括但不限于：LeakyReLU、PReLU、GELU、SELU、SiLU/Swish 以及 ELU 。这些函数通过为负预激活值引入非零激活，提供了不同的权衡。

本文，来自德国吕贝克大学等机构的研究者引入了一种新颖的方法：SUGAR（Surrogate Gradient for ReLU），在不牺牲 ReLU 优势的情况下解决了 ReLU 的局限性。即前向传播仍使用标准 ReLU（保持其稀疏性和简单性），反向传播时替换 ReLU 的导数为一个非零、连续的替代梯度函数（surrogate gradient）。

这样可以让 ReLU 在保持原始前向行为的同时，避免梯度为零的问题，从而复活死神经元。

基于此，本文还设计了两种新型替代梯度函数：B-SiLU（Bounded SiLU）、 NeLU（Negative slope Linear Unit），可以无缝集成到各种模型中。

本研究的进一步贡献如下：

本文对 VGG-16 和 ResNet-18 进行了全面的实验，表明 SUGAR 显著增强了这两种架构的泛化能力。
本文在 Swin Transformer 和 Conv2NeXt 等现代架构上对 SUGAR 进行了评估，展示了其适应性和有效性。
对 VGG-16 层激活的深入分析表明，当应用 SUGAR 时，激活分布发生了明显的变化，为其在缓解消亡 ReLU 问题中的作用提供了直观证据，同时促进了更稀疏的表示。

SUGAR 方法易于实现，并在前向传播中始终采用 ReLU 激活函数。与所提出的 B-SiLU 替代函数结合使用时， VGG-16 在 CIFAR-10 和 CIFAR-100 数据集上的测试准确率分别提升了 10 个百分点和 16 个百分点，而 ResNet-18 与未使用 SUGAR 的最佳模型相比，分别提升了 9 个百分点和 7 个百分点。

论文标题： The Resurrection of the ReLU
论文链接：https://arxiv.org/pdf/2505.22074

SUGAR 介绍

本文提出的方法将 FGI （ Forward gradient injection ）应用于具有平滑替代函数的 ReLU 网络中。在 SUGAR 框架下，FGI 可以表示为：

该公式实现了梯度注入，并确保即使对于负激活也能进行梯度传播。具体来说，利用 [34
中的乘法技巧，替代梯度函数的直接注入如下：

替代函数的选择具有灵活性，可兼容当前最先进的各类激活函数，例如 ELU、GELU、SiLU、SELU 以及 Leaky ReLU（见图 8）。

关键区别在于，与 ReLU 不同，这些候选替代函数均具有一个共同特征：对负输入（x < 0）能产生非零梯度。虽然这些函数为负激活提供了梯度流通路径，但前向传播及后续损失计算仍严格依赖 x > 0 时的激活输出。

在初步研究中，本文意识到需要调整当前的激活函数以适应 SUGAR 的特定用途。因此，接下来本文提出了两个与这些设置良好匹配的新替代函数。

B-SiLU：引入了一种名为 B-SiLU（Bounded Sigmoid Linear Unit）的新型激活函数，它结合了自门控特性和可调下限参数。从数学上讲，该函数可以表示为：

B-SiLU 激活函数的导数为：

图 8 中可视化了 B-SiLU 及其导数。

NeLU：本文进一步引入了 NeLU（Negative slope Linear Unit），作为 ReLU 的平滑导数替代品。

最终的梯度如图 1 所示。

实验

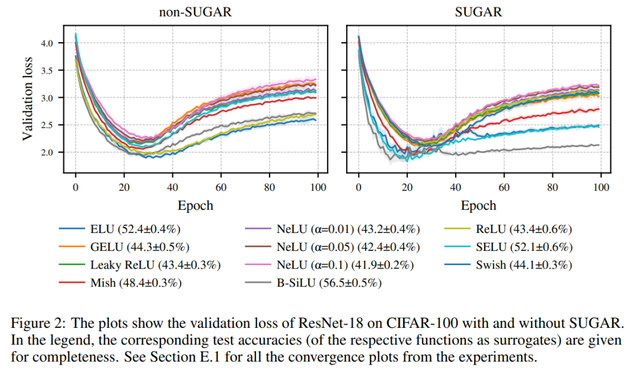
总体而言，与 ReLU 基线相比， SUGAR 结合 ELU、SELU 以及特别是 B-SiLU 获得了最大的提升，而 LeakyReLU 和 NeLU 则始终表现不佳（见图 2）。在 CIFAR-10 数据集上使用 ResNet-18 作为骨干网络时， B-SiLU 的性能从 76.76% 提升到 86.42% ，得益于 SUGAR 。 VGG-16 也表现出类似的效果：B-SiLU 将测试精度提高了近 10 个百分点（从 78.50% 提升到 88.35%）。

在 CIFAR-100 数据集上， SUGAR 结合 B-SiLU 的优势更加明显：ResNet-18 的准确率从 48.99% 跃升至 56.51% ， VGG-16 的准确率从 48.73% 提升至 64.47%（见图 3）。同样， Leaky ReLU 和 NeLU 仅显示出微小的甚至是负的提升（例如 ResNet-18 上的 43.67% → 43.41%）。

总的来说， B-SiLU 在不同架构和数据集上均优于其他替代激活函数， ELU 和 SELU 能够提供可靠的改进，而在这种设置下， SUGAR 从 Leaky ReLU 和 NeLU 中并未获得有意义的益处。

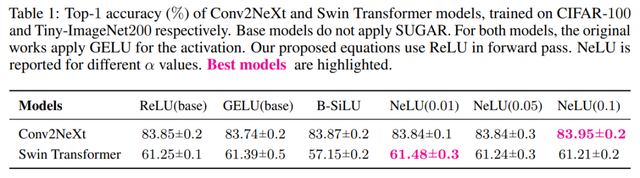
当应用于 Conv2NeXt 时，如表 1 所示， SUGAR 在前向和反向传播过程中均始终优于使用 GELU 的基础模型。

了解更多内容，请参考原论文。